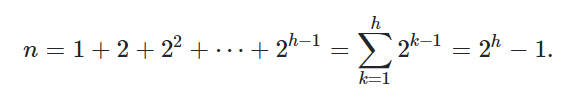공부기록

1. Read chapters 7.1 – 7.7. 7.1 계산 복잡도 계산 복잡도 분석 = 문제의 분석만 의미 (알고리즘 포함X) 비교만으로 정렬하는 알고리즘 (sort only by comparisons of keys) ㄴ> 두 키를 비교하여 어떤 키가 큰지를 결정 가능. 키 저장은 가능하지만 키에 대한 다른 연산은 불가 키의 비교 횟수와 레코드의 저장(assignment) 횟수 기준으로 알고리즘 분석 입력 저장하는데 필요한 저장장소 이외에 + 알고리즘 수행하는데 얼마만큼 추가적인 저장장소 사용하는지 추가 저장장소가 상수면? 제자리 정렬(in-place sort) 항상 비내림차순으로 정렬 (= 그게 오름차순 정렬 아닌지..? 아님! ) 정렬 알고리즘의 출력은 비 내림차순이다. 즉, 이전 원소는 다음 원..

1. Describe linear median finding algorithm. Show that its time complexity is Θ(n). 선형 시간(linear time) : 입력 크기에 비례하여 알고리즘이 실행되는 시간 예를 들어, n개의 원소를 가지는 배열에서 최댓값을 찾는 알고리즘이 O(n)의 선형 시간을 가진다면, 배열의 크기가 2배가 되면 실행 시간도 2배로 증가 ➕ O(n)은 선형 복잡도(linear complexity)라고 부르며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것을 의미한다 ➕ O(n2)은 2차 복잡도(quadratic complexity)라고 부르며, 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미한다. 1️⃣Quick Sele..

Read Chapter 8. 1. Prove that the smallest height for any tree on n nodes is Ω(lg n) = - 1 + lg(n+1). 하한은 높이가 h인 완전 이진 트리를 살펴봄으로써 증명 가능하다. 완전 이진 트리? 높이가 k일 때 레벨 1부터 k-1 까지는 노드가 모두 채워져 있다 (=leaf node가 아닌 모든 노드는 2개의 자식을 가지고 있다) -> 추가 노드를 leaf node에 연결하게 된다면 ? 높이도 증가함. 같은 수의 노드를 가진 이진 트리에서 최소 높이를 가진다! 깊이(h), 노드의 개수(n) h=0, 최대 n=1 h=1, 최대 n=2 (최소 1개) h=2, 최대 n=4 (최소 2개) ... -> 트리의 깊이가 h면, 노드의 개수는 2^..

1. Solve the problems 34 and 40 in chapter.1 a. The solution is provided in the recitation b. Try to solve the problem without the solution and compare. c. What is the difference between your original solution and solution provided? [34] What is the time complexity T(n) of the nested loops below? For simplicity, you may assume that n is a power of 2. That is, n = 2^k for some positive integer k...

1. Download the birthday data. 2. Manually determine the pairs of you who have the same birthday. Explain your method of solution. 생일 값(d) 또한 string으로 입력 받아서 전체 input(n)을 2차원 배열로 만든다. n 배열에 저장된 생일 배열을 비교하면서 순차적으로 탐색한다 ex) [i][0]~[i][3]와 [i+1][0]~[i+1][3] 비교 만약 [0]부터 숫자가 다르다면 탈출 (1,2도 마찬가지) 끝까지 남아있다면? pair로 지정 3. Develop an algorithm for the first question using pseudo code. //1. 몇 명(m)의 생일을 입력할 ..